Hamiltonian Based Circuits

Image

Efficiently calculating the low-lying eigenvalues of Hamiltonians, expressed as sums of Pauli operators, is a key challenge in quantum computing. Variational algorithms offer a promising solution, where trial wavefunctions are prepared on noisy quantum devices using short quantum circuits and iteratively updated to minimize the expectation value of a Hamiltonian. These methods have broad applications in fields, like quantum chemistry, condensed matter physics, and others.

A primary challenge in these algorithms is designing quantum circuits, referred to as ansätze, that are both efficient and effective for this purpose. Current approaches fall into two categories: problem-based ansätze, which leverage the Hamiltonian's structure for accuracy but require impractically deep circuits for NISQ devices, and hardware-efficient ansätze, which are shallow and device-compatible but suffer from scalability and optimization issues, such as barren plateaus.

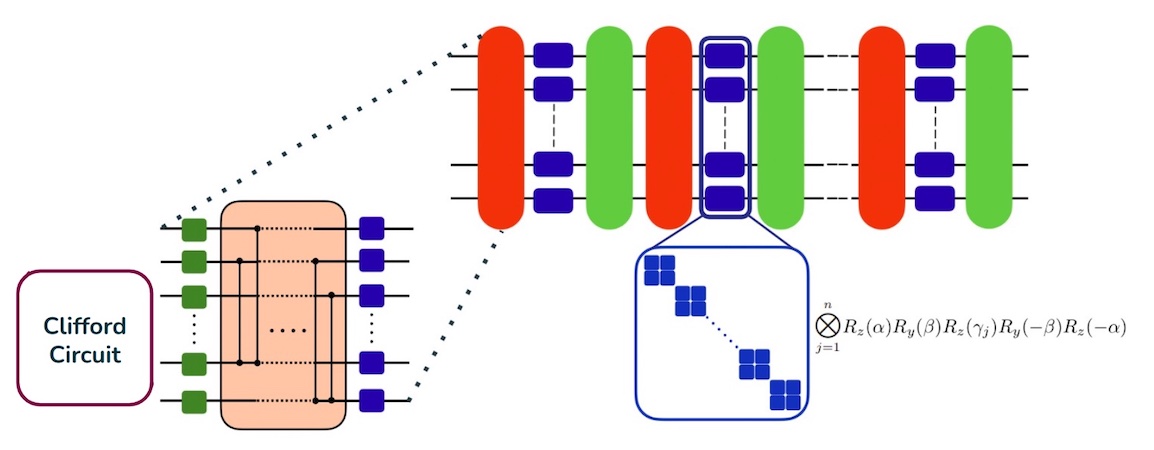
In our work, we address these limitations by combining problem-inspired structures with problem-agnostic layers. We leverage techniques from quantum error correction to design a family of circuits with good trainability and convergence properties. Our approach systematically partitions the Pauli operators in the Hamiltonian into clusters of mutually commuting operators. Each cluster can then be diagonalized using Clifford circuits, as they form a stabilizer group. The Clifford circuits are constructed efficiently using the tableau representation of the Pauli operators. We then approximate the resulting diagonal operators in each cluster by block-diagonal unitaries using a tensor product of arbitrary single-qubit unitaries. The Clifford unitaries, combined with layers of parameterized single-qubit rotations, form the combined-codes ansatz. We provide empirical evidence for the effectiveness of these circuits in accurately determining the ground state energy of different molecular Hamiltonians by carrying out various numerical simulations.

Additionally, by utilizing the correspondence between stabilizer states and graph states, we construct even shorter Clifford circuits, leading to more compact designs. The resulting circuits are referred to as the Hamiltonian-Based Graph States Ansatz (H-GSA). We also conduct numerical simulations with these circuits and demonstrate their accuracy in estimating ground state energies of various molecules, with sizes up to 12 qubits.

The family of parameterized circuits proposed here is low-depth, making them suitable for NISQ devices while maintaining the ability to approximate ground and low-lying excited states. The designs support good initialization strategies, mitigating optimization issues like barren plateaus. While the circuits proposed here are tailored to specific Hamiltonians, the framework can be generalized to other problems. Additionally, this circuit design can naturally support error detection schemes, further enhancing its utility for near-term quantum devices.